回帰分析とは何ですか

「回帰分析」は、結果となる数値と要因となる数値の関係を調べて、それぞれの関係を明らかにする統計的手法です。このとき、要因となる数値を「説明変数」、結果となる数値を「被説明変数」といい、「説明変数」が1つの場合を「単回帰分析」、複数の場合を「重回帰分析」といいます。

回帰分析は、事象の予測・シミュレーション、検証、要因分析などを行うときに用いられ、一般的に

単回帰

重回帰

の式（回帰式）で表されます。

（例）

次のグラフは、あるクラスの男子（A～F）の身長と体重の関係を表したものです。一般的に身長と体重は比例しますが、このグラフからも身長と体重の関係について右上がりの直線のイメージが想像されます。

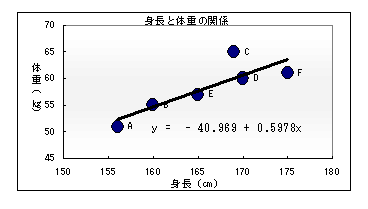
この例で体重と身長を表す式が回帰式で、身長を横軸(x=説明変数)、体重を縦軸(y=被説明変数)とするとy=a+bx（この場合はy=-40.969+0.5978x）とあらわせます。

このような散布図を描いたり回帰式を求めることによって、生徒の身長から体重を予測したり（上の式のxに求めたい生徒の身長の数値を代入する）、Cさんについては、身長に対して体重がやや重めであると推測することができます。